Le Bruit de Dispersion (DITHER)
Pour un signal de fort niveau, l'erreur de quantification est effectivement du bruit. Lorsque le niveau baisse, l'erreur de quantification devient plus fortement corrélée avec le signal, provoquant de la distorsion. Si l'erreur peut, par un moyen ou un autre, être décorrélée du signal d'entrée, le système peut rester linéaire. L'utilisation du bruit de dispersion effectue cette décorrélation en rendant l'action du quantificateur non prédictible. Ce résultat est souhaitable pour un certain nombre de raisons. D'abord parce que le bruit à très bas niveau est subjectivement moins dérangeant que la distorsion ; ensuite, parce qu'il permet souvent aux signaux d'être reconstruits, même lorsque leurs niveaux se situent en-dessous du plancher de bruit du système. Les signaux audio sans bruit de dispersion deviennent couramment "granuleux" et distordus quand leurs niveaux chutent. Un petit souffle résiduel disparaît sans doute si le bruit de dispersion est désactivé mais on considère généralement qu'une petite quantité de souffle continu est largement préférable à une distorsion des signaux de bas niveau.
L'emploi du bruit de dispersion suppose d'ajouter à l'audio un signal de très bas niveau dont l'amplitude et la répartition spectrale dépendent du type de bruit de dispersion utilisé. Le signal du bruit de dispersion est généralement du bruit, mais peut également être une forme d'onde à la fréquence de Nyquist, voir une combinaison des deux.
La question est maintenant de comprendre comment le bruit de dispersion permet de supprimer la distorsion de quantification. Il a été vu précédemment que la distorsion était le résultat de la corrélation entre le signal et l'erreur de quantification : celle-ci rend l'erreur périodique et subjectivement dérangeante. L'ajout de bruit (qui est un signal aléatoire) au signal audio rend l'erreur de quantification aléatoire et le rapproche d'un bruit. Si l'amplitude du bruit est comparable, en niveau, à élément binaire de poids faible, un signal situé exactement au point de décision entre un intervalle de quantification et le suivant peut être quantifié par défaut où par excès en fonction du niveau instantané du bruit de dispersion qui lui est ajouté. Dans le temps, cet effet aléatoire est moyen ; il produit d'une part une erreur de quantification de type bruit, d'autre part un plancher de bruit fixe dans le système.
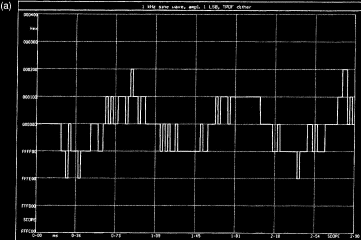
En (a), on retrouve la même onde sinusoïdale d'amplitude ± 1 LSB que dans
la page précédente mais cette fois avec ajout de bruit de dispersion
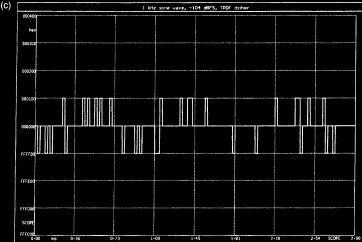
analysée dans la domaine numérique. On observe en (b) le spectre de cette
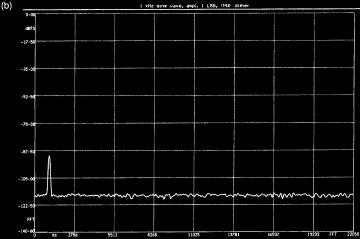
onde avec bruit de dispersion. En (c), on observe une onde sinusoïdale à un
niveau de -104 dBFS avec bruit de dispersion montrant une modulation occasionnelle
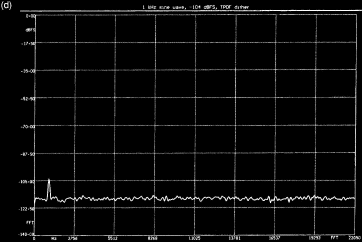
du LSB. En (d), le spectre de ce signal montre qu'il est encore possible de
discerner le signal d'origine. Un système 16 bits sans bruit de dispersion
serait incapable de représenter un signal de niveau inférieur à -97 dBFS environ.
La figure ci dessus (a) représente la même onde sinusoïdale de très bas niveau que celle de la figure de la page précédente mais, cette fois, avec ajout de bruit de dispersion. Comme on l'observe sur le spectre (b), le signal quantifié conserve le sinus à 1 kHz ; celui-ci montre une partie d'onde sinusoïdale isolée accompagnée d'un plancher de bruit plat. Les figures (c) et (d) montrent également la forme d'onde et le spectre d'une onde sinusoïdale avec bruit de dispersion ; le niveau de la forme d'onde est tel qu'il serait absolument impossible de la représenter avec un système 16 bits sans bruit de dispersion. Le LSB se trouve à l'état 0 beaucoup plus fréquemment mais, si l'on regarde avec attention, un élément de la période d'origine à 1 kHz est encore visible sur son graphe de modulation. Le cycle de travail de la modulation de l'élément binaire de poids faible (LSB) (rapport entre les durées à l'état haut et à l'état bas) varie avec l'amplitude du signal d'origine. Lorsque celui-ci passe par un convertisseur analogique/numérique et par un filtre de reconstruction, on obtient un signal sinusoïdal pur avec du bruit, comme on peut le constater sur l'analyse spectrale.
La première utilisation du bruit de dispersion ayant fait l'objet d'une publication eut lieu dans le domaine du codage de l'image. Dans le système utilisé, le bruit ajouté avant quantification était soustrait après la conversion en analogique. Ce procédé porte le nom de bruit soustractif (substractive dither). Bien qu'une telle soustraction présente quelques avantages, elle souffre d'inconvénients, en pratique, dans la mesure où le bruit d'origine doit être transmis en plus des échantillons, ou recréé de façon synchrone par le convertisseur numérique analogique. Ceci est pratiquement impossible dans un système où les signaux ont fait l'objet d'un montage. En pratique, les appareils utilisent un bruit non soustractif, qui est ajouté avant quantification, sans tentative ultérieure de l'éliminer. L'introduction du bruit de dispersion est source, inévitablement, d'une légère diminution du rapport signal/bruit possible, mais cette dernière est le prix à payer pour obtenir l'élimination des non-linéarités. Cette linéarité est un critère essentiel dans le domaine audio.
Sur la figure suivante, nous voyons qu'on peut ajouter linéairement du bruit soit au signal d'entrée, soit à la tension de référence dont découlent les intervalles de quantification.
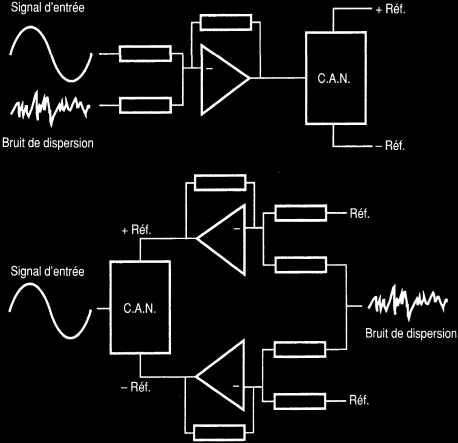
Il y a différentes façons de considérer l'action du bruit de dispersion. L'ajout de ce dernier implique que des échantillons successifs rencontreront des intervalles de quantification disposés différemment sur l'échelle des tensions. L'erreur de quantification deviendra une fonction du bruit de dispersion et plus seulement du signal d'entrée. Elle ne sera pas supprimée, mais la distorsion produite, perceptivement inacceptable, sera transformée en un bruit à large bande, plus bénin. Ce bruit peut aussi faire l'objet d'une mise en forme spectrale en vue de tenir compte des caractéristiques de réponse en fréquence de l'oreille.
Une autre façon de voir les choses est de considérer la situation où le signal de faible amplitude évolue lentement à l'intérieur d'un intervalle de quantification. En l'absence du bruit de dispersion, le même code numérique est toujours reproduit, et les variations sont perdues. Le bruit de dispersion a pour effet d'obliger la quantification à osciller entre deux états, ou plus. Plus la tension d'entrée est élevée dans l'intervalle, plus il est probable que la donnée codée passera à une valeur supérieure. Plus la tension est faible dans l'intervalle, plus il est probable qu'elle passera à une valeur inférieure. Le bruit de dispersion a en quelque sorte opéré une modulation non périodique qui a permis d'étendre la résolution du système, qui n'est alors plus limitée par les pas de quantification.
On peut aussi expliquer l'action du bruit de dispersion en examinant ses conséquences sur la fonction de transfert du quantificateur. Cette dernière est normalement un escalier parfait, mais, en présence du bruit, elle est brouillée dans le sens horizontal, de telle façon qu'avec une certaine amplitude la fonction de transfert moyenne devient linéaire.
Les caractéristiques du bruit utilisé sont importantes pour obtenir des performances optimales. Les paramètres les plus importants sont la valeur crête à crête de son amplitude, ainsi que sa distribution fréquentielle. Les recherches ont montré que certains types de bruit de dispersion conviennent mieux que d'autres aux applications audio de haute qualité. Le bruit de dispersion est souvent caractérisé en termes de distribution de probabilités ; cela consiste en une méthode statistique montrant la "propension" d'un signal à avoir une certaine amplitude. Un graphe simple du type de la figure suivante est employé pour indiquer la forme de la distribution. L'axe vertical représente la probabilité et l'axe horizontal l'amplitude en termes de pas de quantification.
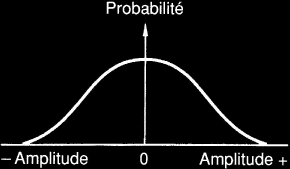
Cette courbe de distribution de probabilités associée au bruit de dispersion
montre les chances du signal d'avoir une amplitude donnée.
Lorsque le bruit de dispersion est utilisé, les règles de calcul habituelles du rapport signal/bruit pour une longueur de mot donnée ne peuvent plus s'appliquer. Cela est pratiquement sans conséquences dans la mesure où la règle simplifiée qui énonce que multiplier le nombre d'éléments binaires du mot par 6 dB donne le rapport signal à bruit conduit à des résultats suffisamment précis dans toutes les situations concrètes. Cette technique est également utilisée lors de la conversion de signaux quantifiés sur un certain nombre d'intervalles vers un système à résolution moindre.
La Méthode de Conversion DELTA SIGMA
Il existe différentes technologies pour réaliser des convertisseurs analogiques-numériques. J'ai ici choisi de considérer cette méthode particulière appelée Delta-Sigma parce que c'est celle qui est utilisée dans la plupart des convertisseurs qu'ils soient analogique/numériques ou l'inverse. Elle est encore appelée Bitsream conversion ou autre selon les appétits commerciaux. Elle utilise le suréchantillonnage. Les convertisseurs utilisant la méthode Delta-Sigma, initialement développés pour le domaine du son, existent maintenant sous forme de Codec (Codeur-décodeur) dans les cartes son des ordinateurs, ainsi que dans les systèmes de télécommunication numériques et la téléphonie. A ce jour, ils sont de plus en plus utilisés dans les cartes d'acquisition de signaux et d'instrumentation.
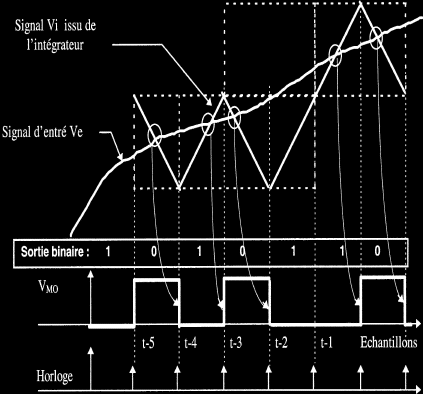
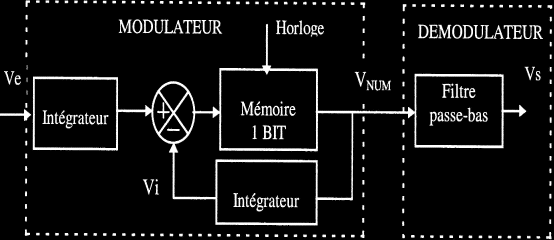
Le principe est basé sur la modulation Delta. Ce type de modulation consiste à obtenir en sortie du montage un signal rectangulaire dont le rapport cyclique est l'image de l'amplitude du signal d'entrée. L'intérêt de cette modulation apparaît au niveau de la démodulation, car il suffit d'un intégrateur pour retrouver le signal d'origine. Dans le principe, cette modulation consiste, non pas à réaliser une quantification absolue par rapport à zéro, mais à mesurer la différence entre deux échantillons successifs (aux temps t et t-1) puis d'en déduire une valeur 0 ou 1. La modulation Delta est représentée par la figure suivante où nous retrouvons les fonctions de comparaison, d'intégration et de mémorisation.
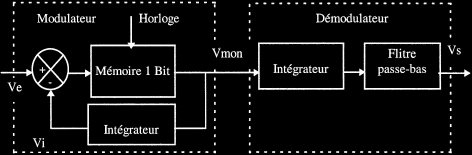
Schéma (I) fonctionnel de la modulation Delta.
Pour analyser le principe de fonctionnement, rappelons tout d'abord que la tension de sortie Vmon est de forme rectangulaire, son rapport cyclique variable est fonction de l'amplitude du signal d'entrée Ve.
Le comparateur analyse Ve avec la tension Vi. Comme nous le verrons plus loin, la tension Vi correspond à la tension de sortie de l'intégrateur. Elle s'apparente à la tension Ve à la différence qu'elle n'est pas continue mais composée de successions de pentes ascendantes et descendantes. La démodulation est réalisée uniquement par un intégrateur et un filtre passe-bas.
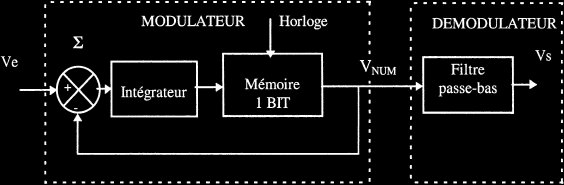
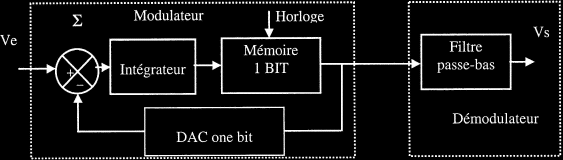
Le schéma précédent représente uniquement le principe de la modulation et de la démodulation Delta. Le signal Vmon est de type rectangulaire (le rapport cyclique est l'expression de l'amplitude du signal Ve). Mais afin d'obtenir une valeur binaire, image de l'amplitude du signal d'entrée, un traitement numérique est ajouté au montage. Cette fonction est appelée filtre digital ou filtre de décimation (illustrée à la figure suivante).
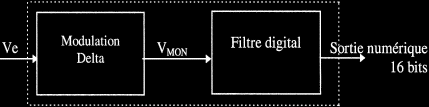
Convertisseur (16 bits) basé sur la modulation Delta.